|
|
|
|
|
As a preamble to many of the more complicated logical strategies it is worthwhile understanding how cells ‘see’ each other. This allows us to use more familiar language than technical terms like ‘overlaying’ or ‘congruence’. There are 81 cells in a normal Sudoku and they all belong to one row, column and box. Any cell can always ‘see’ all eight other cells in the box they reside in, plus six other cells in the row and column, making a sphere of influence of 20 cells. Consider R2C2 in this diagram. |
 |
All the shaded cells in this diagram can be ‘seen’ by the black cell at R2C2.
Any solution at this cell excludes the same number from the other twenty cells. |
 |
If we add a second cell there will be two or more cells that both cells can ‘see’, in this case R2C6 and R5C2.
The overlap between the two is show in the cross hatch. |
|
| |
Many of the more interesting and advanced strategies use links or chains of conjugate pairs (candidates that occur just twice in a row, column or box). This is a vital trick and we will use it to build some very sophisticated rules. To start with, let’s look at a theoretical example: |
|
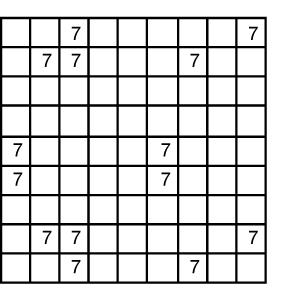
Fig. 17.1 |
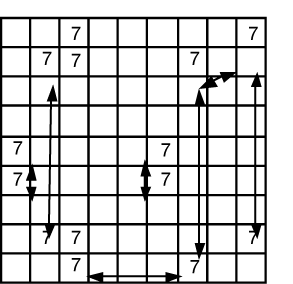
Fig. 17.2 |
|
Here all the numbers have been removed except candidates 7 (the known solutions for 7 have also been removed). |
Next we look for all the pairs for 7 and join them with double arrows. |
|
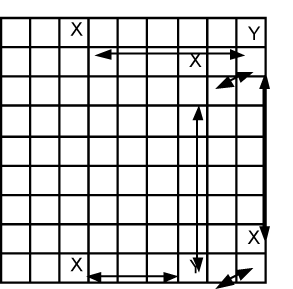
Fig. 17.3 |
Some of these arrows (or links) are isolated and not interesting. However, One chain of links connects six pairs. When we ‘colour’ these pairs we pick one cell (say in A3) and choose a colour. We follow all the links alternating with another colour. In a black and white book I can’t use colour so I’ve used the letters X and Y. |
|
| |
|
|
What we are saying when we do this is that either all X or all Y must be 7.
When we have a pair of candidates we are have two possible logical statements:
Either
X => !Y (If X is 7 then Y is not 7)
Or Y => !X (If Y is 7 then X is not 7)
All we have done with Colouring or Chaining these pairs is extend the length of the statement.
A3 => !A9 => H9 => !J7 => J3
Or !A3 => A9 => !H9 => J7 => !J3
Our chains of X and Y are mutually exclusive possible positions for the number 7 solely because they are formed by pairs. Now how is all this useful? If there is a candidate 7 which is on the chain or even somewhere else on the board that can see both an X and a Y (or two cells with different colours) then that candidate can be eliminated. Another way of looking at this is we’ve proved that either X or Y must be a 7 so there is no possibility that another 7 can exist on any cell that X and Y can both “see”. |
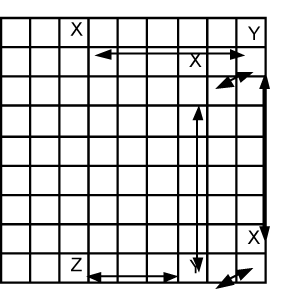
Fig. 17.4 |
Visiting our diagram again I’ve change the letter for 7 in J3 to Z.
It represents a 7 that can “see” both the X in A3 and the Y in J7.
We can remove this candidate. Because Z is part of a pair-chain a cascade of events follows. J7 must be a 7 so B7 and H9 cannot be (remove the 7’s there) and A9 must be 7 so A3 cannot be. |
|
From this we get two very important rules:
Our first rule is: Whenever two cells in a singles chain have the same colour and also share the same unit, that colour must be the 'false' colour since each unit can only have one of any candidate value.
In our diagrams above we had two X’s in the third column, ie two cells with the same colour. That allows us to falsify all X’s according to this rule and the cascade effect is proved.
Our second rule is: whenever a candidate outside the chain relates by column, row or box to two alternately coloured cells in a singles chain, that 'non-chain' candidate can be excluded. This applies to Z above if we consider the Z not part of the chain but a clearer example of a ‘non-chain’ elimination is below. (Our number is 1): |

Fig. 17.5 |

Fig. 17.6
|
We can start a chain of pairs at F1 and alternately colour the cells formed the links.
Although there are a lot of ones on the board we can find one 1 at C5 which can see two differently coloured cells at C7 and E5. This can be safely removed. |
|
|

Fig. 17.7 |
There is a ridiculously long chain using the number 9 on this board which contains twelve links. The alternating colours have been marked. You have to find this chain and mark which candidate 9 is eliminated. It uses the second rule so the 9 that’s eliminated is not on the chain. |